できるだけ丁寧にGANとDCGANを理解する

目的

  • Chainerの扱いに慣れてきたので、ニューラルネットワークを使った画像生成に手を出してみたい
  • いろいろな手法が提案されているが、まずは今年始めに話題になったDCGANを実際に試してみるたい
  • そのために、 DCGANをできるだけ丁寧に理解することがこのエントリの目的
  • 将来GAN / DCGANを触る人の助けになったり、理解間違ってるところにツッコミがあると嬉しい

本エントリの構成

  1. DCGANの前提となっているGANの論文の要点をまとめる
  2. DCGANでGANとの差分として提案されている要点をまとめる
  3. DCGANのmattyaさんの実装を読み通して詳細を理解する

1. GANについて

  • GANは、サンプル群と似たような性質を持つ出力を生成するためのフレームワーク
  • 2014年にIan J. Goodfellowらによって提案された

  • 論文: Generative Adversarial Nets [リンク]

  • 以下の2つのモデルの訓練を同時に進め、互いに競わせる

    • D: Discriminator(鑑別器): （生成したいサンプルとGの出力物を正しく鑑別できることを目指す）
    • G: Generator(生成器):（ランダムノイズを入力として、Dが誤ってサンプルであると認識する率を高めることを目指す）
  • GANは下記の式の価値関数V(G, D)で表現されるminimaxゲームとして定義できる
 
\begin{eqnarray} 
\min_{G}\max_{D} V(D, G) =  \mathbb{E}_{x \sim p_{data}(x)}\big[\log D(x)\big] +  \mathbb{E}_{x \sim p_{z}(x)}\big[\log (1-D(G(z)))\big]
\end{eqnarray}
  • この式を、前提含め日本語で書き下してみると
[前提]
・ p_zはある種の任意の分布（例えば一様分布）を表す。zは個々のノイズサンプルを表す。
・Gはzを入力とし、 p_gに分布させる。 p_gはジェネレータGから生成された出力の分布を示す
・Dは入力がサンプルから来た確率を表す(1であれば入力はサンプル分布 p_xから、0であればGの出力分布 p_gからと判断)
[左辺]
・価値関数Vは関数DとGを引数に取る、右辺で表される関数である
・Dについての最大、Gについての最小となるようD, Gを定める
[右辺]
・確率変数xは確率分布 p_{data}に従う
・確率変数zは確率分布 p_zに従う
・このとき、 log D(x)の期待値と、 log(1-D(G(z)))の期待値の和を評価関数とする
（Dがサンプルを正しくサンプルと判定できれば log D(x)が大きくなり、DがGの出力をサンプルだと判定すると log(1-D(G(z)))が小さくなる）

となる。（と思うのですが、間違っていたらご指摘いただければ嬉しいです..）

  • この式自体は、G、Dがニューラルネットワークであることを前提とはしていない（言い換えれば、別な関数最適化手法であっても適用できる、かもしれない）

  • 論文ではD, Gにニューラルネットワークを使うことで、既存の最尤推定による生成モデルで手に負えないほど計算量が増える問題をbackpropagationで回避できるとしている

  • 論文掲載のアルゴリズムは下記となる

    1. ミニバッチサイズm個のノイズ {z_1}...{z_m}を p_g(z)から取り出す（生成する）
      (論文は p_gからになってるけど、 p_zの誤植のような..?）
    2. ミニバッチサイズm個のサンプル {x_1}...{x_m}をデータ生成分布 p_{data}(x)から取り出す
    3. 下記式の、 \theta_d における確率的勾配を上るように鑑別器Dを更新する
      \begin{eqnarray} \frac{1}{m}\sum_{i=0}^m \big(\log D(x^{(i)}) + \big(\log (1 - D(G(z^{(i)} ))) \big) \end{eqnarray}
    4. 上記までをk回繰り返す
    5. ミニバッチサイズm個のノイズ {z_1}...{z_m}を p_g(z)から取り出す (ここも p_zが正しいような..?）
    6. 下記式の、 \theta_g における確率的勾配を下るように生成器Gを更新する
      \begin{eqnarray} \frac{1}{m}\sum_{i=0}^m \log (1 - D(G(z^{(i)} ))) \end{eqnarray}
    7. ここまで全てを、訓練回数分だけ繰り返す

  • 鑑別器Dを十分な回数(k回)更新した上で生成器Gを1回更新することで、常に鑑別器が新しいGの状態に適用できるように学習を進める

  • 4.1 ~ 4.2 [tex: p_g = p{data} ] の時にD, Gそれぞれについての最適化が達成される
    ==> このため、 p_g を [tex: p    {data} ] に近似させることが上記評価関数の解への近似として正当化される

  • 利点と欠点

    • 欠点: 明示的な p_g が最初は存在せず、DはGとシンクロさせて訓練しなければならない （特に、DをupdateせずにGだけを訓練すると、Gが入力ノイズzの多くをxと同じ値に収束させてしまう点に注意）
    • 利点:
      • マルコフ鎖で複数のモデルを混ぜるためにぼやけたものになるが、GANではマルコフ鎖が不要でシャープな画像が生成できる。
      • 勾配を得るためにBPが使えるため、学習に近似が不要。
      • 様々なモデルを用いることができる
      • そして何より、「計算可能(computational)である」。
      • サンプルと直接比較するのではなく、Discriminatorの評価を介して生成するため、inputの部品をGがそのまま丸覚えすることを避けられる。

2. DCGANについて

  • GANは具体的なネットワークの構成に言及していない。（少なくとも論文中では）
  • DCGAN(Deep Convolutional Generative Adversarial Networks) は、GANに対して畳み込みニューラルネットワークを適用して、うまく学習が成立するベストプラクティスについて提案したもの。
  • 元になった論文 Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks リンク
  • 要点をまとめると下記のようになる
    • プーリング層を全て下記で置き換える
      • D(鑑別器): 畳み込み層（strided convolutions）(これはいわゆる普通の畳み込み層のことらしい)
      • G(生成器): 分数的にストライドする畳み込み層 (fractional-strieded convolutions)(これはすなわちdeconvolution a.k.a. transposed convolutionsのことらしい...)
    • バッチノルムを使用する（重要らしい）
    • 深い構成では全結合層を除去する
    • 生成器ではReLUを出力層以外の全ての層で活性化関数として使用し、出力層ではtanhを使用する
    • 識別器ではLeakyReLUを全ての層で使用する

3. DCGANのコードを読む

前処理

  • import / 定数宣言は解説省略
  • image_dirから全てのイメージを読み込んで、dataset配列に追加している。
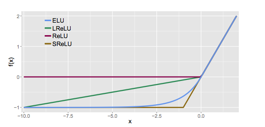
  • ELU: exponential Linear Unitの定義。 数式でいうと \alpha > 0の元で
 
\begin{eqnarray} 

f(x) = \left\{
\begin{array}{ll}
x  & \text{if }  x > 0 \\
\alpha(\exp(x)-1) & \text{if } x \leq 0
\end{array}
\right.
,
f'(x) = \left\{
\begin{array}{ll}
1  & \text{if }  x > 0 \\
f(x)+\alpha & \text{if } x \leq 0
\end{array}
\right.

\end{eqnarray}

グラフでいうと

f:id:mizti:20161210164101p:plain （出典: Djork-Arne Clevert, Thomas Unterthiner & Sepp Hochreiter 2016 https://arxiv.org/pdf/1511.07289v5.pdf )

となるもので、LeakyReLUをなめらかにした感じのものらしい。

Generatorの定義:

  • 一様分布ノイズz(1次元 / 100要素)を入力として、
    => 100入力、66512 出力のLinear Unit で(100, 512, 6, 6 )に=> BatchNormalization => relu => => 512チャネル入力、256チャネル出力、pad1、stride2、フィルタサイズ4のDeconvolution2D で(100, 256, 12, 12)に=> BN => relu
    => 256チャネル入力、128チャネル出力、pad1、stride2、フィルタサイズ4のDeconvolution2D で(100, 128, 24, 24)に=> BN => relu
    => 128チャネル入力、64チャネル出力、pad1、stride2、フィルタサイズ4のDeconvolution2D で(100, 64, 48, 48)に=> BN => relu
    => 64チャネル入力、3チャネル出力、pad1、stride2、フィルタサイズ4のDeconvolution2D
    として、最終的に(100, 3, 96, 96) （つまり、ミニバッチ100枚 x RGB3チャネル x w96 x h96）のデータが得られる。

Discriminatorの定義:

  • サンプルイメージ or Gの出力(3, 96, 96)を入力として、
    => 3チャネル入力、64チャネル出力、pad1、stride2、フィルタサイズ4のConvolution2Dで (64, 48, 48)に => 上述のELU
    => 64チャネル入力、128チャネル出力、pad1、stride2、フィルタサイズ4のConvolution2Dで(128, 24, 24)に => BN => ELU
    => 128チャネル入力、256チャネル出力、pad1、stride2、フィルタサイズ4のConvolution2Dで(256, 12, 12)に => BN => ELU
    => 256チャネル入力、512チャネル出力、pad1、stride2、フィルタサイズ4のConvolution2Dで(516, 6, 6)に => BN => ELU
    => 512 x 6 x 6 入力、2出力の全結合層

訓練

  • Gの訓練
    • Gの訓練時の入力zは、-1から1の間で一様分布の (100 x 100 )二次元のランダム値
    • Gからの出力xをDの入力とする
    • Dの出力ylは「Dが入力をGのものだと思う確率」を示している（元論文とは逆に設定されてるので注意） 　すなわち、Dの出力が0であればデータセットからの出力、1であればGが"偽造"した出力と判断
    • Gの損失: ylとbatch数だけ並んだ0とのソフトマックスクロスエントロピー関数出力(ylが全て0であれば損失なし)
    • Dの損失: ylとbatch数だけ並んだ1とのソフトマックスクロスエントロピー関数出力(ylが全て1であれば損失なし)
  • Dの訓練
    • x2をDの入力にして、yl2を出力。
    • Dの損失に「yl2とbatch数だけ並んだ0とのソフトマックスクロスエントロピー関数出力」を足し合わせる
  • 勾配初期化とbackpropagateによる重み更新
  • image_save_interval回の訓練毎にGENを使って画像を100枚。
    この際の生成のタネにする乱数は訓練開始前に生成したzvisを常に利用する
  • 毎epoch完了ごとにdis, gen, o_dis, o_genを保存

わからなかった点

  • 何故Discriminatorが「2つ」の出力を持つようにしているのかわからない。入力の p_{data}かららしさだけを出力するのなら、1出力でよさそうに思えてしまう。損失関数の計算方法から見るに、どちらか1つの要素がG、もう一つがdataからの入力というわけでもなさそうに思える。

その他