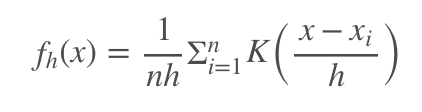Apache2.2から2.4へのhttpd.confの記載方法変更

書いてあること

Apache2.2から2.4に乗り換える必要があったためhttpd.confの記載変更点をまとめた。

 

詳細は

https://httpd.apache.org/docs/2.4/upgrading.html

を参照。

変更点

 

	2.2での記法	2.4での記法	備考
アクセス管理記法が変更された	Order deny,allow Deny from all	Require all denied
	Order allow,deny Allow from all	Require all granted
	Order Deny,Allow Deny from all Allow from example.org	Require host example.org
	Order Deny,Allow Allow from all AuthType Basic AuthBasicProvider file AuthUserFile /example.com/conf/users.passwd AuthName secure Require valid-user	AuthType Basic AuthBasicProvider file AuthUserFile /example.com/conf/users.passwd AuthName secure Require valid-user	ユーザ単位の認証が記載されている場合、Host単位の認証は省略可能（Deny, Allow扱い）
	Order allow,deny Deny from all # Satisfy ALL is the default Satisfy ALL Allow from 127.0.0.1 AuthType Basic AuthBasicProvider file AuthUserFile /example.com/conf/users.passwd AuthName secure Require valid-user	AuthType Basic AuthBasicProvider file AuthUserFile /example.com/conf/users.passwd AuthName secure <RequireAll> Require valid-user Require ip 127.0.0.1 </RequireAll>	ホスト認証＋ユーザ認証を併用する場合はRequireを<RequireAll>で囲って併記する記法を用いる
変数名の変更	MaxRequestsPerChild	MaxConnectionsPerChild
	MaxClients	MaxRequestWorkers
廃止	DefaultType	-
デフォルト挙動の変更	AllowOverride		デフォルトの挙動がNoneに（.htaccess ファイルが無視される）
	EnableSendfile		デフォルトでOFFに
	FileETag		デフォルトでOFFに
パラメータの変更	KeepAlive		OnかOffのみを受け付けるように （以前は0がOffに、それ以外の文字はOnの代替として挙動）
モジュールの変更	mod_dav_fs		DavLockDB ファイルのフォーマットが変更されているため古いファイルは削除する必要あり
	mod_cache		CacheIgnoreURLSessionIdentifiers が部分一致ではなく完全一致に変更
	mod_cache		2.2以前では/がすべてのコンテンツとマッチしたが、マッチ範囲が厳密に
	mod_ldap		LDAPTrustedClientCertがディレクトリ単位の設定のみに変更
	mod_filter		FilterProvider の記法が変更（ブール記法で判定）
	mod_include		・#if expr 記法が新しい文法に変更 ・ディレクトリスコープのSSI*設定が他のディレクトリのSSI*設定を上書きしないように
	mod_charset_lite		DebugLevelが廃止されモジュール単位のLogLevelで設定する形に
	mod_ext_filter		同上
	mod_proxy_scgi		PATH_INFOのデフォルト設定が変更
	mod_ssl		CRLに基づくrevocation checkingはSSLCARevocationCheck による明示的な設定が必要に
	mod_substitute		最大のline長が1MBに
	mod_reqtimeout		モジュールロード時に幾つかのデフォルトのタイムアウトを設定
	mod_dumpio		DumpIOLogLevel のサポートが終了し、LogLevelがtrace7に固定

スタイル変換系論文サーベイ(1)

画像変換、特にStyle変換の論文を読んでまとめていく。随時追記。

---

A Neural Algorithm of Artistic Style

URL

https://arxiv.org/abs/1508.06576

発表月

2015/8

どんなもの？

・NNをスタイル転写に用いることができることを初めて示した論文。

先行研究に比べて良い点

類似の専攻研究への参照なし

技術・手法のキモ

・学習済みVGG19のパラメータを固定、スタイル画像とコンテンツ入力画像を入力とし、下記の損失関数を最小化するようにホワイトノイズを入力Backpropにより修正していく

モデルと損失

・NNの構成 VGG19をコンテンツ画像、スタイル画像、生成画像に対して利用

・損失の構成 コンテンツ損失: コンテンツ画像と生成画像のあるl層での特徴量の二乗和

スタイル損失: 2つの行列の相関関係を表すグラム行列

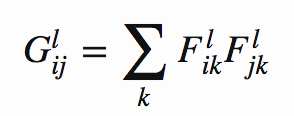
を考え、スタイル画像と生成画像それぞれのグラム行列の二乗平均誤差を

(Gはスタイル画像のグラム行列、Aは生成画像のグラム行列) とする。この E_l の各層での重み付き和をスタイル誤差とする

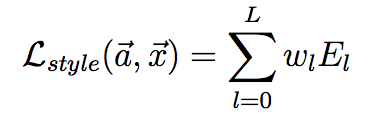
これら2つの誤差の重み付き和

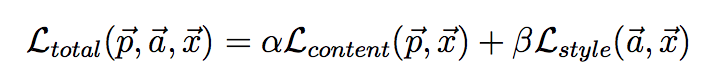
を最小化の対象とする。

有効性検証の方法

• ( 定量的な方法ではなく、様々な画像のスタイル変換を示すことにより)

議論/留意点

・スタイル適用済み画像を生成するためにNNの訓練と同様にBackpropを要するため、非常に時間がかかる

・最適化手法、重み付け方等で様々な改善が後に提案されている

不明点・分からなかったこと

特になし

---

Perceptual Losses for Real-Time Style Transfer and Super-Resolution

URL

https://arxiv.org/abs/1603.08155

発表月

2016/3

どんなもの？

・A Neural Algorithm of Artistic Styleが提案したスタイル変換をfeed forwardネットワークによりリアルタイムで実施する方法を提案

・超解像度等の画像変換タスクでも従来の"per-pixel"損失を設定した研究に比べ感覚的によりよい結果を得られた

先行研究に比べて良い点

・Semantic SegmentationやDepth Mappingなどの画像変換タスクではピクセルごとの損失(Per Pixel Loss)やCRF Lossを用いていているが、groud-truthとアウトプットの間の「感覚的な(perceptual)」違いを捉えることはできていなかった。

・Gatysらは知覚に沿った損失(Perceptual Loss)を設定し直感的に優れたスタイル変換を達成したが、Backpropにより画像を変換するため生成に時間がかかる

=> 本研究では、両者の良いところを兼ね備えた

1. (Per-PixelやCRFでは不可能な) 感覚的な違いを捉えることができ
2. feed-forwardにより素早い変換が可能な

手法を提案している

技術・手法のキモ

・画像クラス識別用に事前訓練されたCNNが感覚的/意味的な情報を抽出できることを活かして、損失関数の計算に用いる。（ImageNet訓練済みVGG16）（この点は先行研究と同様）

・直接styleやcontentをpixel単位で比較するのではなく、損失計算用NNのそれぞれの層の出力を比較して損失を計算し、Feed ForwardなNNを訓練する

モデルと損失

モデルの全体構成

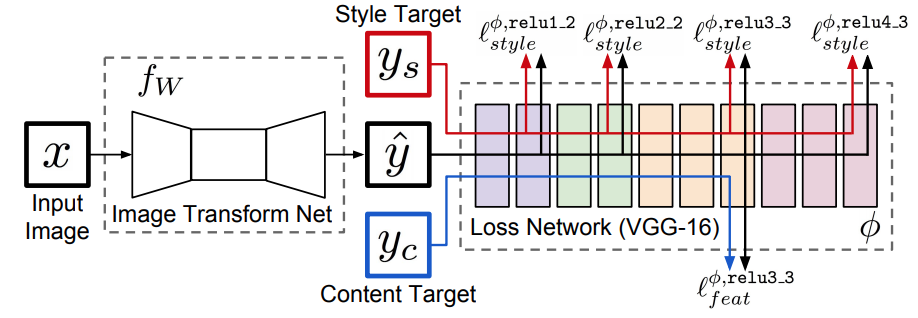
上記NNで、 x: 入力画像 y_s: スタイル画像 y^: xをƒwによって変換した画像 y_c: コンテンツ画像 とする。（スタイル変換では、xとy_cに変換したい画像を、y_sにスタイル対象の画像を入力する）

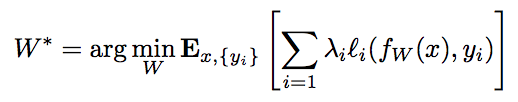
そして、各層で計算された損失の期待値を最小化するƒの重みWを訓練によって獲得する。

• ƒwの構成: Deep Residual Learning for Image RecognitionでResidual Deep CNNを5層重ねて構成する。
• Encoderとして残差付きConvolutionを用いる
• Decoderとして残差付きfractionally strided convolutions(=Deconv)を用いる
• pooling層は用いない
• 非線形関数にはReLUを用いる。
• ただし出力層にはtanhを用いる（0~255の範囲に出力を限定するため）

損失

特徴再現損失:

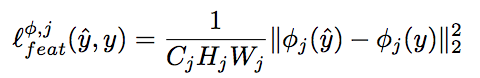
（ここではyはy_c）

スタイル再現損失: グラム行列

に対して、

をスタイル再現損失とする。（ここではyはy_s）

これらの重み付き和を最小化する。

上記の他にも、論文内で超解像度への適用も行っているが、ここでは省略。 有効性検証の方法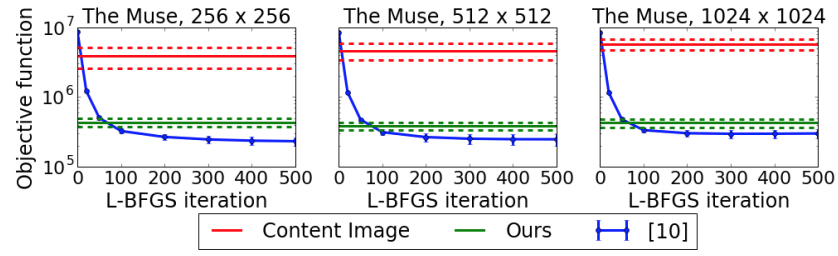 ・定量的にはGatysらの手法に対して、目的関数の差がほぼ同じオーダーに収まることを示した

・また、変換速度についてはGatysらの手法に比べて1000倍近く早いことを示している。 ・定性的には、MS COCOの各種画像をstyle変換した結果を示している。

議論/留意点

・一つのスタイルに対して一つのƒwの訓練を要する ・スタイル変換以外にも超解像度にも適用可能（着彩やsemantic segmentationはfuture workとしている） ・別のデータセットやタスクで訓練された損失計算NNを用いることで、また異なった意味もった生成を行える可能性もある

不明点・分からなかったこと

次に読むべき論文

---

Let there be Color!: Joint End-to-end Learning of Global and Local Image Priorsfor Automatic Image Colorization with Simultaneous Classification

URL

http://www.f.waseda.jp/hfs/colorization_sig2016.pdf

発表月

2016/7

どんなもの？

• 白黒の写真画像を自動的に着彩する
• 融合層（"fusion layer"）を導入したことにより、小さな画像に依存する局所的な情報と画像全体から算出される大域的な事前分布をうまく同時に考慮し、既存手法より自然な着彩が可能
• どのような解像度の画像でも着彩可能

先行研究に比べて良い点

• 全体的(global)な情報と部分的(local)な情報を両方考慮したEnd-to-Endな自動着彩（人手による指定一切不要）
• どんな大きさ(解像度)の画像でも処理できる / ラベルを学習に用いることが出来る

技術・手法のキモ

• Globalな特徴を抽出するネットワーク、Localな特徴を抽出するネットワークで別々に画像から特徴を抽出し、それらの結果を融合させるFusion Layer
• Pooling層、FC層を使わないFully Convolutionalな構成(global feature network以外)
• global featureとラベル識別を同時に並行して訓練する訓練手法

モデルと損失

モデル:

• Low Level Feature Network(紫)

Convolution層のみからなる。Global Featureの抽出の入力としても同じ重みのNWを利用する。

f:id:mizti:20180121210600p:plain、以下同じ)

• Global Feature Network(茶色)

ConvとFCからなる。FCを含むため、入力サイズを確定させておく必要があり、このためGlobalへの入力を生成するLow-Levelへの入力画像は224x224にリサイズしておく。

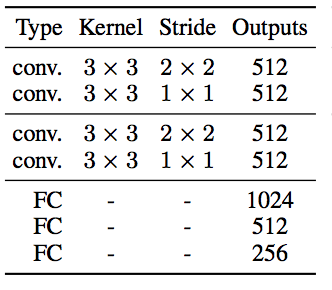
• Mid-Level Feature Network(青色)

Convのみからなる。

• Fusion Layer(赤点線)

Global層の出力と、Mid層の出力を結合したものを入力として1層のFCを適用

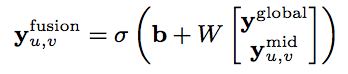<= 重要

• Colorization Netowrk(緑色)

Deconvolutionを使わず、ConvolutionとUpsampling(Nearest Neighbor)のみからなるデコーダ。

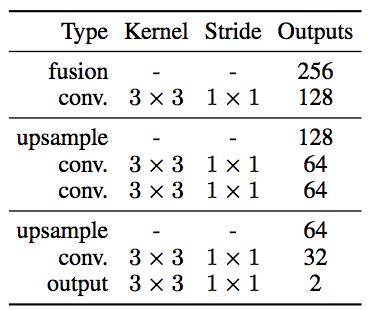
画像はLabカラー形式で扱っているため、L(明度≒モノクロ)を入力とし、出力はaとb*となる。

• Batch Normalizationは訓練時のみ適用、訓練終了後は重みに繰り込み

• 活性化関数はReLU, 最終層はSigmoid

損失:

画像の着彩誤差と同時にラベル識別誤差を足す。

y_colorは二乗和平均(MSE)、y_classはクロスエントロピー (双方が同じ程度の影響になるように、α=1/300程度で設定) （|| ||はフロベニウスノルムの意）

訓練:

最適化アルゴリズムはADADELTAを採用。233万枚の訓練画像をバッチサイズ128で20万イテレーション(11epoch)。256x256にリサイズした画像から毎回224x224でクロップ、50%で左右反転。

有効性検証の方法

・SotAな手法(Cheng2015)、Global Feature無しの着彩、提案手法の3点で着彩を行い、ユーザによる「自然に見える」割合を調査

議論/留意点

• Global Featureのみを別の画像を入力とすることで、全体的なスタイルの転移が可能 （ただし、Semanticにある程度共通点のある画像であることが必要）
• RGB、Lab、YUVの各表色系を比較し、Labが一番良さそうということで採用
• 訓練データにまったく含まれないようなタイプの画像（人の描いたものなど）は上手く着彩できない

不明点・分からなかったこと

• 「Batch Normalizationは訓練時のみ適用、訓練終了後は重みに繰り込み」の具体的な方法

次に読むべき論文

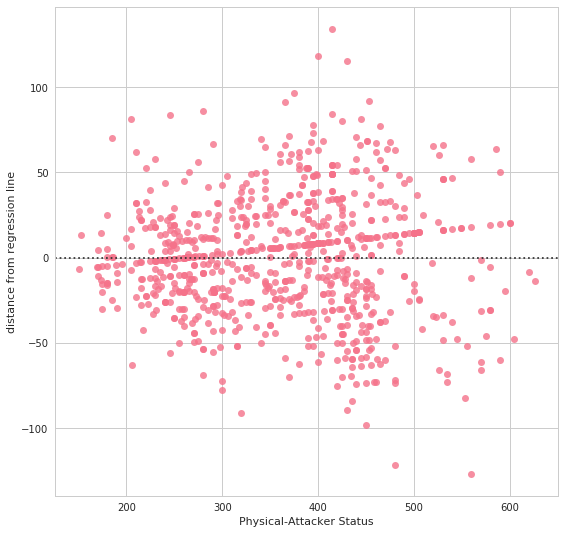
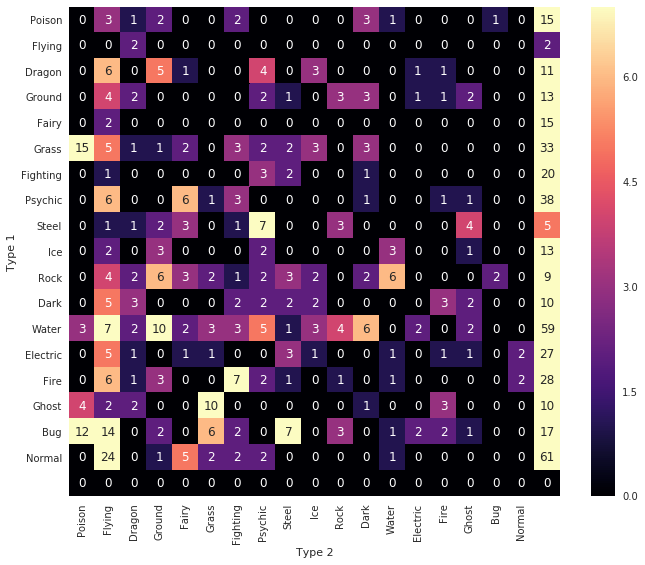
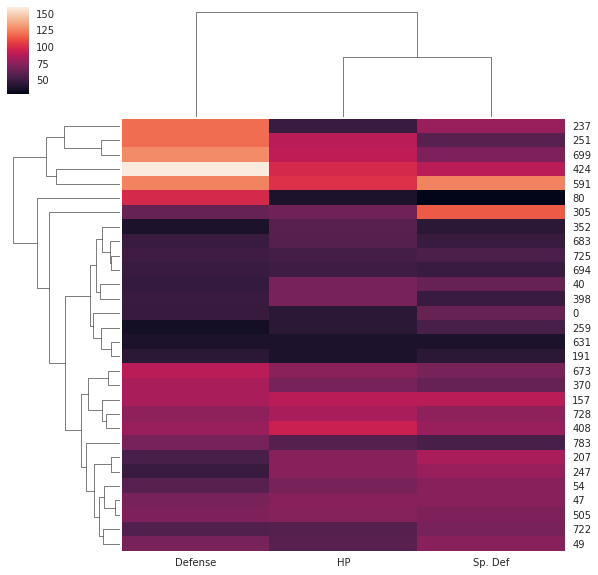
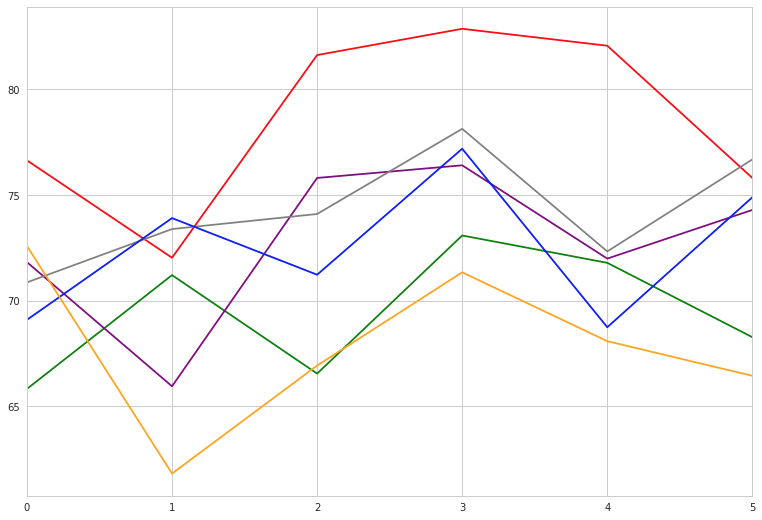
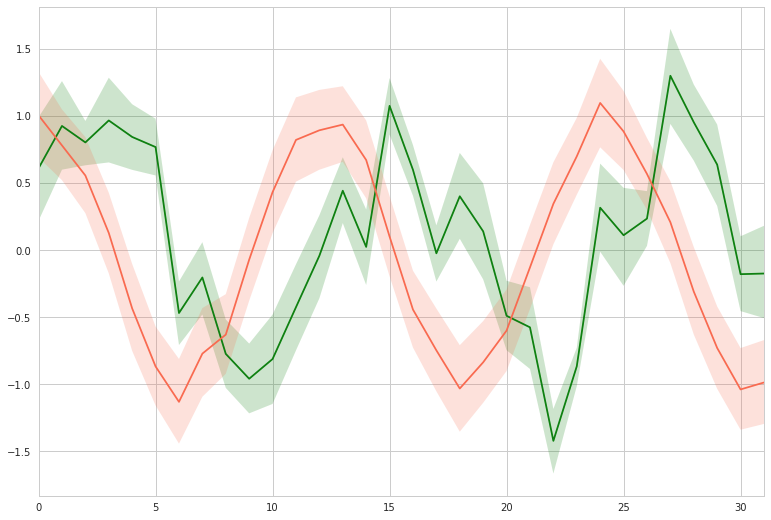
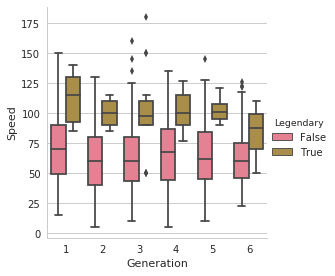
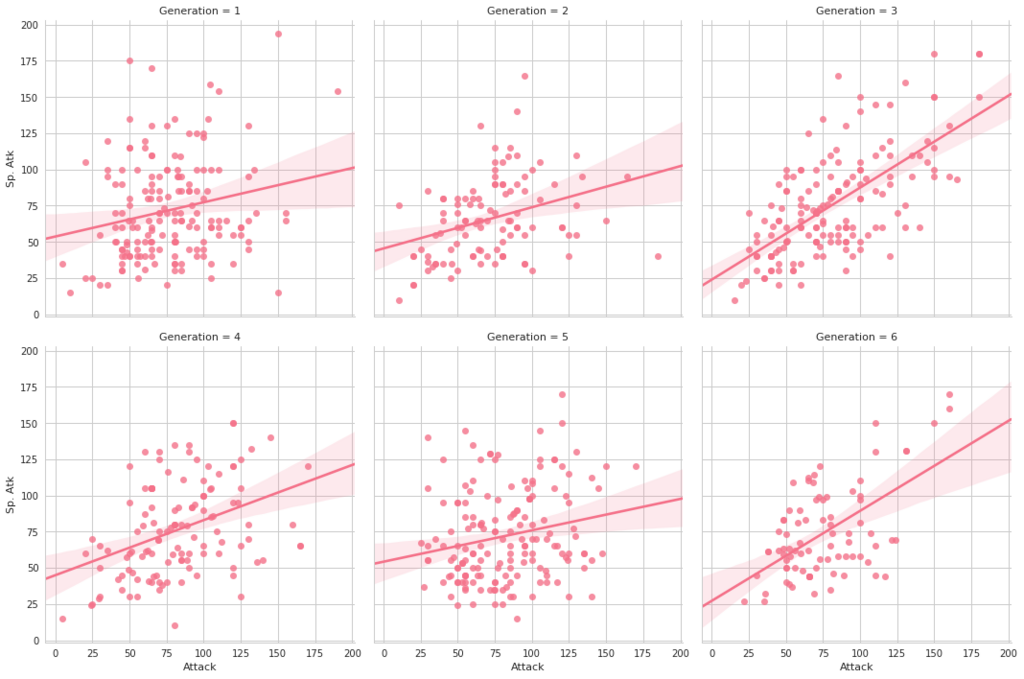
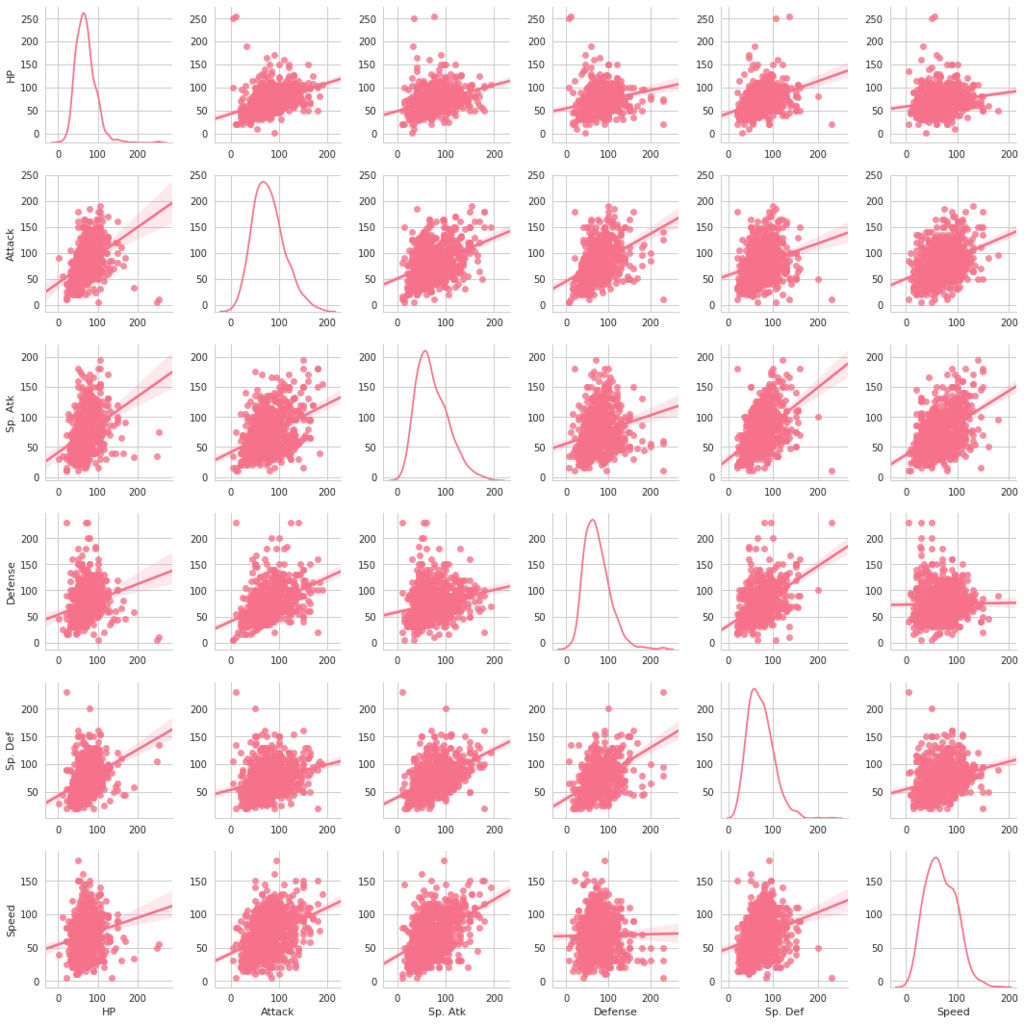
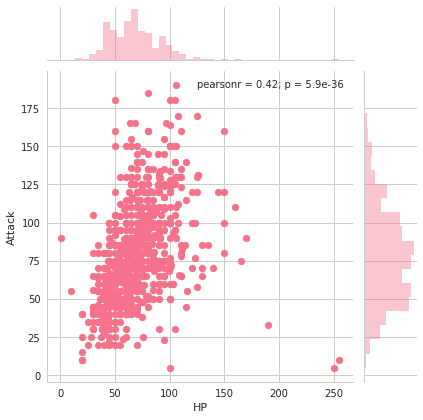
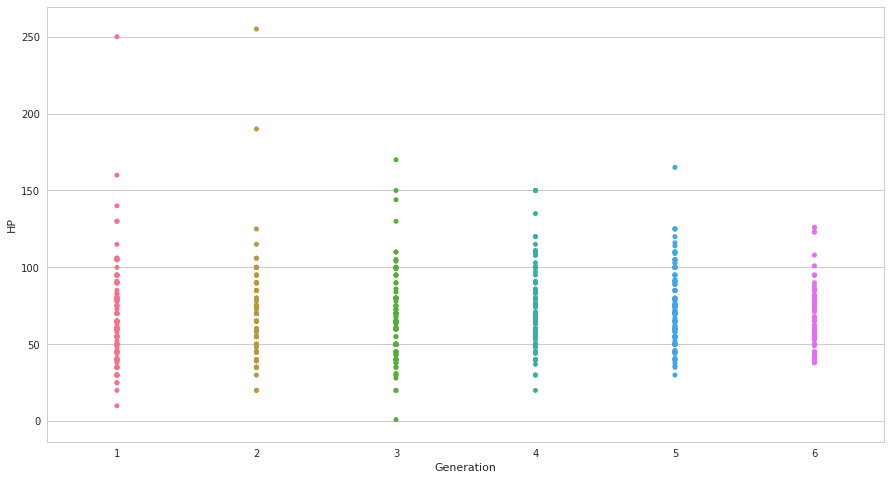
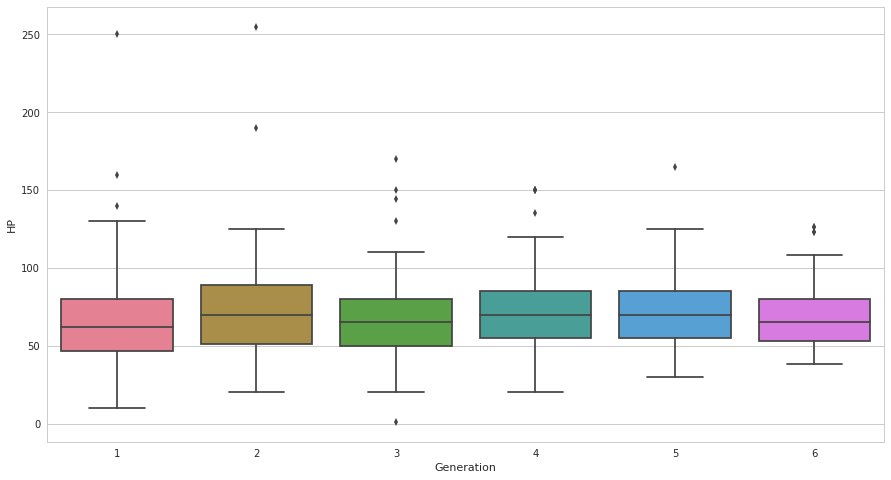
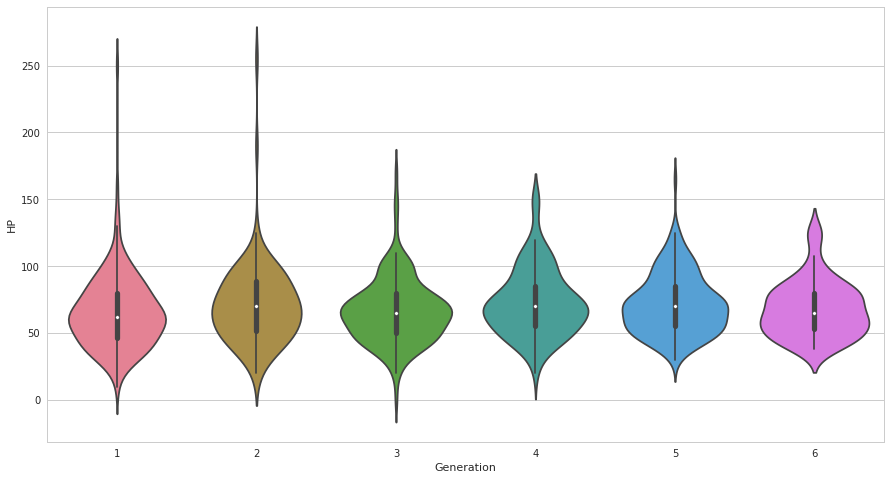
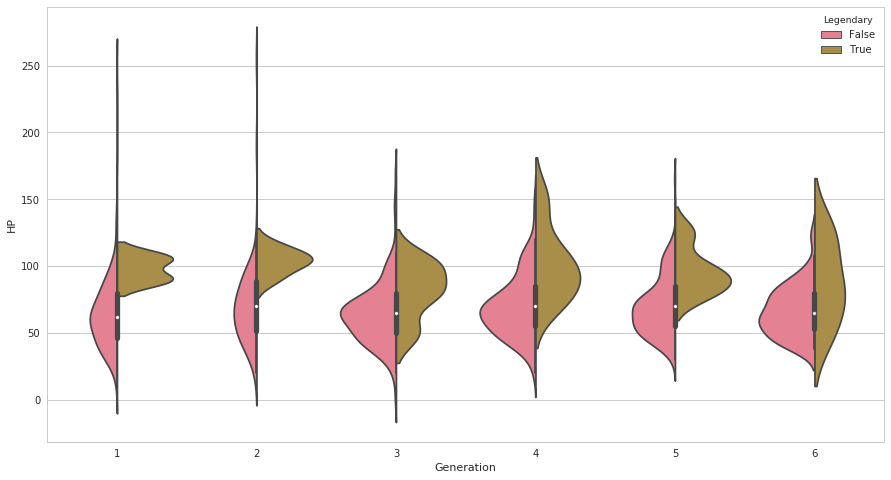
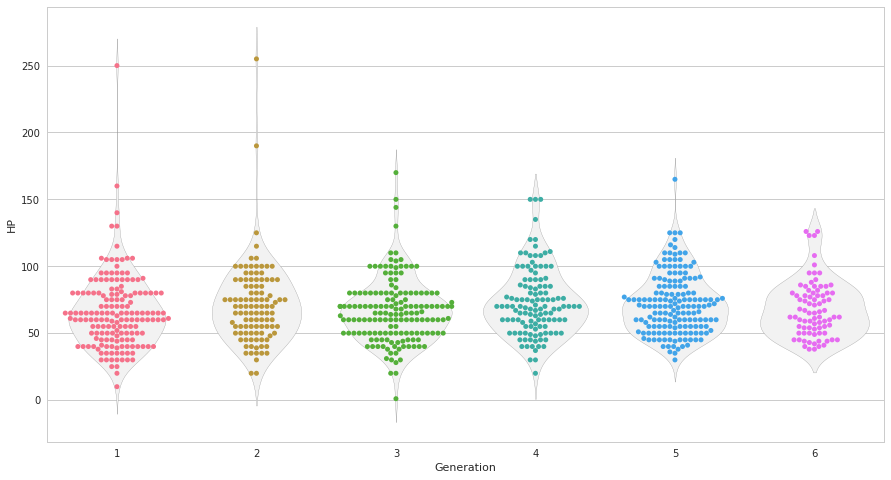
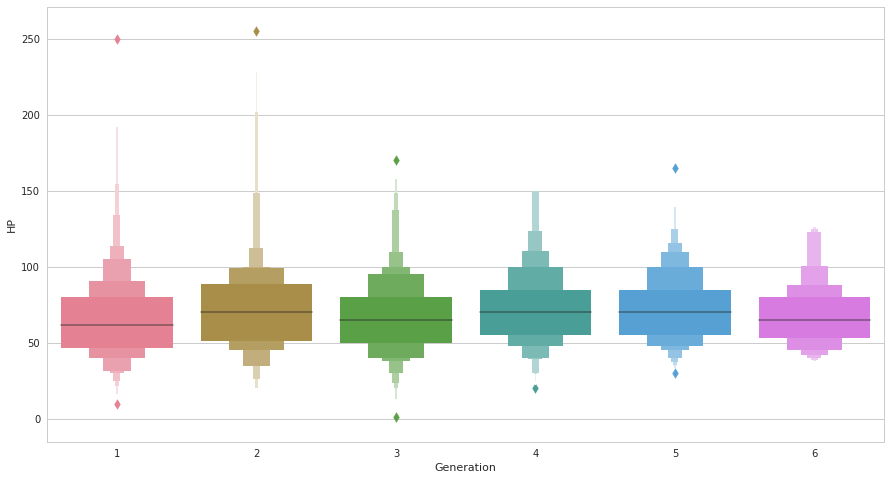
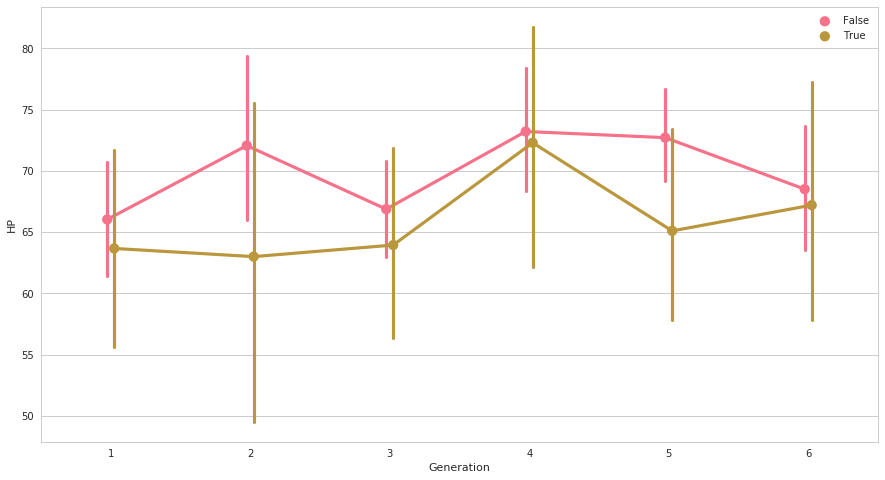
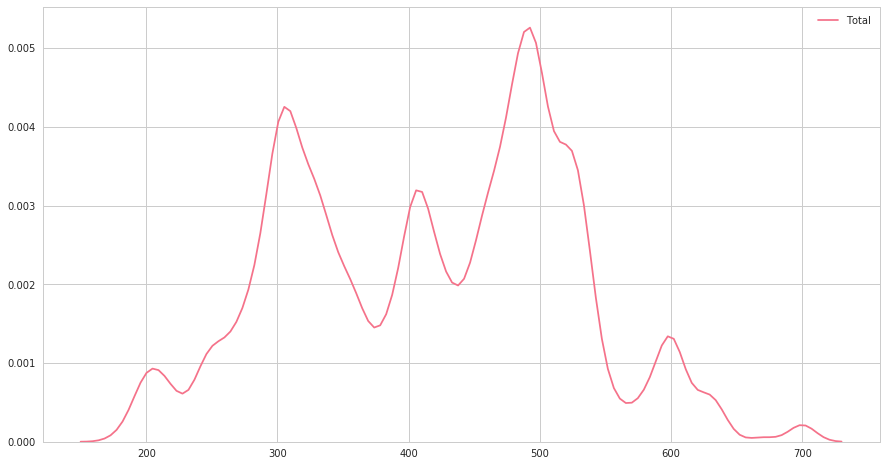
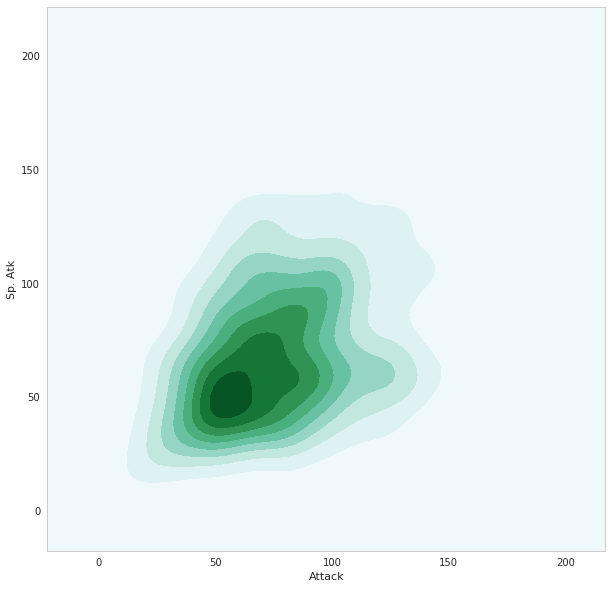
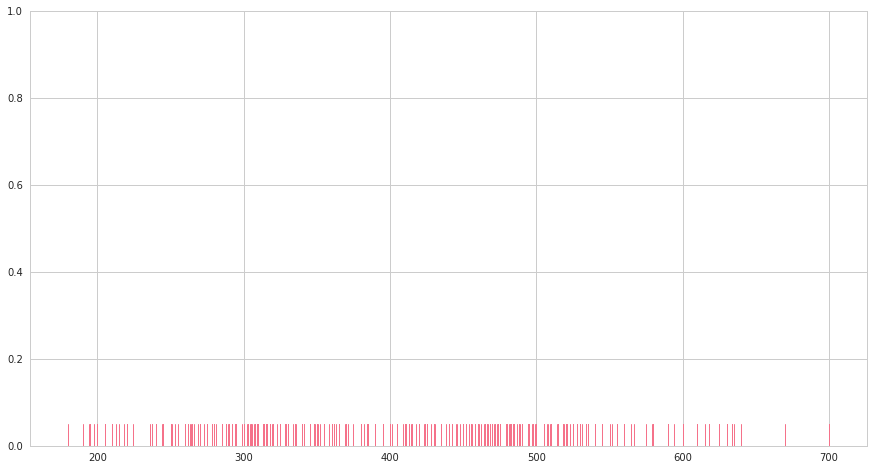
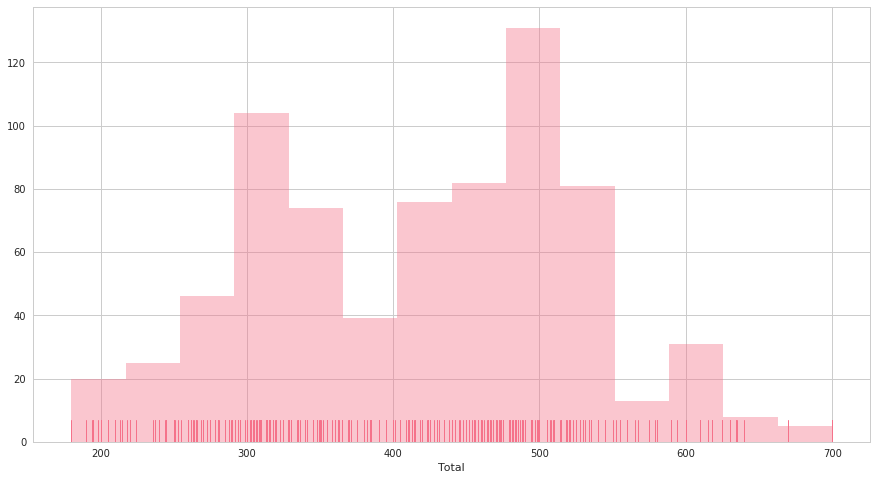
seabornによる統計データ可視化（ポケモン種族値を例に）(2)

前記事の続きです

mizti.hatenablog.com

3. Regression plots

２つの系列のデータを受け取り、回帰や残差を可視化します。回帰を可視化するregplotと残差を可視化するresiplotがあります。

regplot

plt.figure(figsize=(9, 9))

ax = sns.regplot(x=(pkmn["Total"] - pkmn["Sp. Atk"]), y=(pkmn["Total"] - pkmn["Attack"]))

d = ax.set(xlabel='Physical-Attacker Status', ylabel='Sp-Attacker Status') # d is just for supressing output

 

regplotでは与えられた2つのデータから散布図を描き、回帰線を引きます。 散布プロットと回帰線の有無はそれぞれscatter / fit_regパラメータで切り替え可能です。

上記ではステータス合計値 "Total" から特殊攻撃力/攻撃力を引いた値をそれぞれX軸/Y軸とし、物理攻撃アタッカー性能/特殊アタッカー性能としてプロットしてみました。

デフォルトでは回帰の方法は線形回帰(order=1の多項式回帰)となっていますが、多項式回帰の次数を増やすことができます。また、yに真偽値を入れてlogistic=Trueを指定することでロジスティック回帰を用いることも可能です。

plt.figure(figsize=(9, 9))

ax = sns.regplot(x=pkmn["Total"] , y=pkmn["Legendary"], logistic=True)

 

伝説のポケモン(y=1.0)とそれ以外(y=0.0)で分類し、ロジスティック回帰を行いました。

回帰線の周囲にある薄い色付きの領域は信頼区間で、デフォルトでは95%です。ciパラメータで%を指定することができます。今回のデータの場合は全てのサンプルが網羅されているのであまり意味がありませんが、母集団からの標本によって作ったデータの場合は、100回のサンプリング群のうち95回はこのピンク色の範囲に回帰線が含まれるだろう、と見ることができます。 

residplot

plt.figure(figsize=(9, 9))

ax = sns.residplot(x=(pkmn["Total"] - pkmn["Sp. Atk"]), y=(pkmn["Total"] - pkmn["Attack"]))

d = ax.set(xlabel='Physical-Attacker Status', ylabel="distance from regression line") # d is just for supressing output

 

residplotは残差を散布図としてプロットします。（残差、とは予測値とデータの離れ具合を指す統計上の用語です）

すこし分かり辛いですが、y=0の線が線形回帰線にあたり、そこからどのくらい離れているかがy軸になっています。 何らかの回帰を行ったあとで、回帰線からの離れ方がx軸の系列とどのような関係にあるか見るのに適しています。

ここでは、上記のregplotの最初で書いた線形回帰と同じデータの残差を可視化してみました。

線形回帰だとregplotを見れば普通は十分ですが、多項式回帰などで回帰線が複雑な曲線を描くような場合には残差の分布がわかりづらくなるため、有用に使えると思います。 

4. Matrix plots

Matrix plotsは、複数のカテゴリデータ同士の関係を可視化します。

heatmap

 

s2 = pkmn["Type 2"]

labels2, levels2 = pd.factorize(s2)

labels1 = levels2.get_indexer(pkmn["Type 1"])

s = np.zeros*1

for i in range(len(labels1)):

    if(labels2[i]<0): # assign "N/A" as 18th in table

        labels2[i] = 18

    s[labels1[i] ,labels2[i]] += 1

 

plt.figure(figsize=(11,9))

ax = sns.heatmap( s, vmin=0, vmax=7, annot=True, cmap="magma", xticklabels=levels2, yticklabels=levels2)

d = ax.set(xlabel='Type 2', ylabel='Type 1') # d is just for supressing output 

heatmapはその名の通り受け取った配列をヒートマップで可視化します。

今回はタイプ同士の組み合わせ分布を可視化してみました。

データ解析周りでheatmapを一番良く使うのは、分類問題で予測ラベル/正解ラベルの組み合わせを可視化するケースだと思います。(この利用方法の場合、confusion matrixなどとも呼ばれます)

予測が正解に完全に一致していれば左上から右下に綺麗に赤いが一直線に並び、そこからはみ出した部分は予想誤りということになります。

色温度の組み合わせは用途に合わせて https://matplotlib.org/examples/color/colormaps_reference.html から自由に選択してください。

clustermap

import random

st = pkmn.loc[:, ['HP', 'Defense', 'Sp. Def']].sample(30, random_state=179)

plt.figure(figsize=(11,9))

ax = sns.clustermap(st, metric='euclidean', method='average') 

clustermapは、指定されたデータセットについて類似度によってクラスタリングを行った結果をデンドログラムで表示します。（各データについてはヒートマップのように色付けを行いながら）

例ではポケモンのHP / 防御力 / 特殊防御力を基準として類似度の近い者同士が近くなるように描画しています。 あまり数や次元が多いと計算に時間がかかるため、ランダムに抜き出した30種類に絞っています。

metricオプションによって、各データをベクトルと見做したときの、二つのデータ間の類似度の測り方を指定できます。例えば、 metric='euclidean' であればユークリッド距離、 metric='cosine'であればコサイン類似度によって、といった具合です。

詳細はこちら: https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.pdist.html

また、methodオプションではクラスター同士をどのように結合していくかの規則を指定できます。 例えば、method='single'であれば、あるクラスターを結合する先を選ぶ際に、両方の含まれる最も近い点同士の距離が最も小さいクラスターと、method='average'であればクラスターに含まれる全てのデータ同士の距離の平均が最も小さいクラスターと結合されます。

詳細はこちら: https://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.linkage.html

実際に活用する場合では、素のデータをそのままクラスタリングするのではなく、何らかの形で特徴量抽出を行った上でクラスタリングすることが多いと思います。

 

5. Timeseries plots

tsplotの一種類のみです。時系列データを描画します。

tsplot

v = ["HP","Attack","Sp. Atk","Defense", "Sp. Def", "Speed"]

mean = pkmn.groupby(["Generation"])["HP","Attack","Sp. Atk","Defense", "Sp. Def", "Speed"].mean()

#std = pkmn.groupby(["Generation"])["HP","Attack","Sp. Atk","Defense", "Sp. Def", "Speed"].std()

plt.figure(figsize=(13,9))

ax = sns.tsplot(mean["HP"], color="Green")

ax = sns.tsplot(mean["Attack"], color="Red")

ax = sns.tsplot(mean["Sp. Atk"], color="Purple")

ax = sns.tsplot(mean["Defense"], color="Grey")

ax = sns.tsplot(mean["Sp. Def"], color="Blue")

ax = sns.tsplot(mean["Speed"], color="Orange") 

tsplotは文字通り時系列を可視化するためのplotです。

あまり時系列になりそうなものがなかったのですが、一応世代を時系列とみなして各ステータスの平均の推移をプロットしてみました。 これだけではあんまりなので、もう一つ、データを生成してプロットしてみます。

x=np.linspace(0,16,32)

sin = np.sin(x) + np.random.normal(0, 1.2,  (16,32))

cos = np.cos(x) + np.random.rand(16, 32) + np.random.randn(16, 1)

 

plt.figure(figsize=(13,9))

 

ax = sns.tsplot(sin,color='Green')

ax = sns.tsplot(cos,color='Reds')

それぞれsin, cosに対して正規分布や一様ランダムを加えて動きを与えたプロットです。 今回の場合で先程と異なるのは、各時系列に対して各系列16ずつの値のばらつきを持っていることです。このような場合、実線は各時の平均となり、信頼区間は色付きで表されます。(デフォルトでは68%信頼区間)

6. Miscellaneous plots

文字通り、「その他」のプロット。palplot一つしかありません。 

palplot

plt.figure(figsize=(15, 8))

ax = sns.palplot(sns.color_palette(n_colors=24), 2)

ax = sns.palplot(sns.color_palette("Set1", 24))

ax = sns.palplot(sns.color_palette("terrain", 5))

ax = sns.palplot(sns.color_palette("terrain", 8))

ax = sns.palplot(sns.color_palette("terrain", 15))

ax = sns.palplot(sns.color_palette("inferno", 15))

 

palplotはデータ可視化用のプロットではなく、現在設定されているパレットの内容を確認するためのプロットです。 特に他者にデータを可視化する場合、見やすかったりデータのイメージに合った色を選ぶのが重要になるので色の調整等に 使いましょう

http://seaborn.pydata.org/tutorial/color_palettes.html

 

7. Axis grids

最後はAxis gridsカテゴリです。

このカテゴリは若干特殊で、複数の変数の組み合わせに対して今までにあげたplotを描くための枠を用意し、一度にグラフを描けるseabornを"便利に"使うためのツールがまとまっています。 このため、このカテゴリは上記で見てきたplotをオプションで指定して利用するものが多く含まれています。 

Facet Grid

plt.figure(figsize=(16,16))

g = sns.FacetGrid(pkmn, col="Generation")

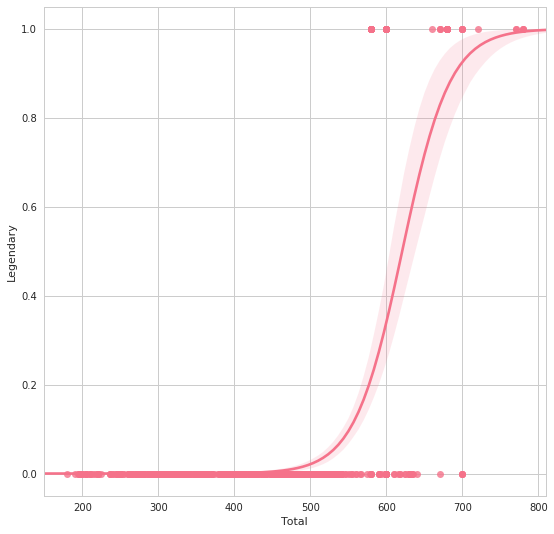
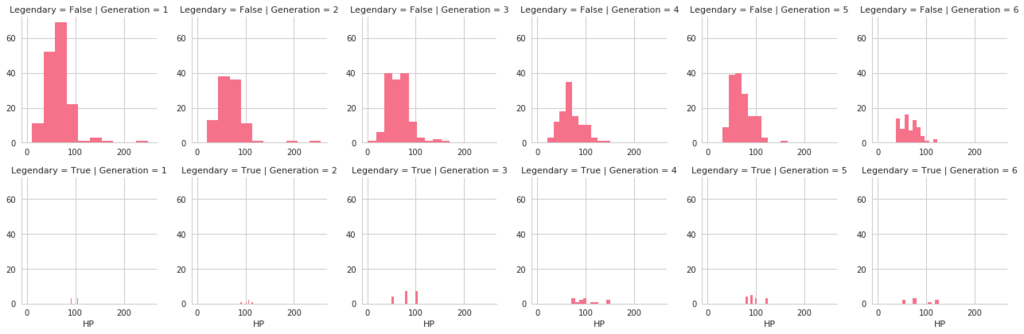  FacetGridは、指定した要素ごとにプロット領域を定義するクラスです。これ単体ではプロットは行われません。 （matplotlibに馴染みのある人であればsubplotをまとめて定義してくれる、と表現すればわかりやすいかもしれません） FacetGridは後述のfactorplot, lmplotで継承されて利用されているようです。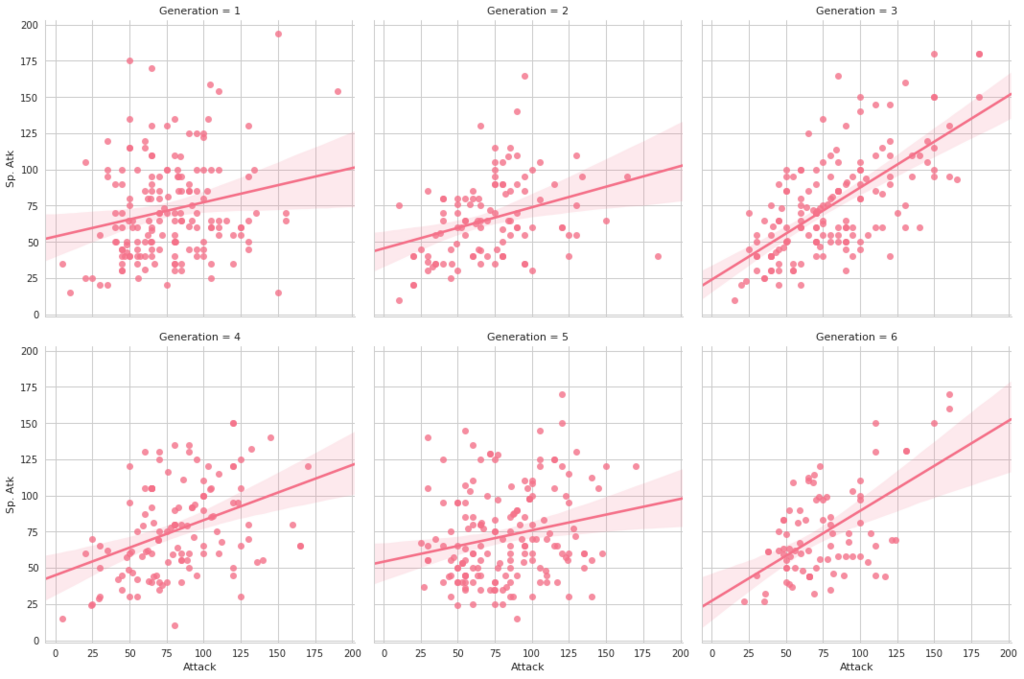

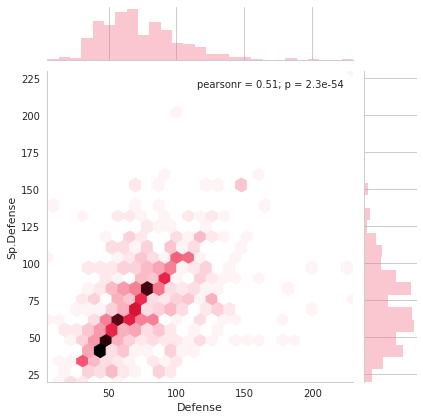
rowパラメータにより横軸に展開する要素を、colパラメータで縦軸に展開する要素を指定できます。

In [32]:

plt.figure(figsize=(16,16))

g = sns.FacetGrid(pkmn, col="Generation", row="Legendary")

g = g.map(plt.hist, "HP")

FacetGridを代入した変数(上記ではg)にmapを適用することによって、matplotlib等でグラフを描画することもできます。

上の例では上段が非伝説、下段が伝説で、左から順にGenerationごとのHPの分布を可視化しています。 

factorplot

plt.figure(figsize=(16,16))

g = sns.factorplot(x="Generation", y="Speed", hue="Legendary", data=pkmn, kind="box")

 

上の方の例でviolineplotやpointplotで、複数系列を同時に描画した例がありました。factorplotは、「複数の系列を同時に描画する」という目的でseabornの各種プロットを整理して呼び出せるようにしたもの、と考えられます。

対象にしたい連続値が一つで、多数のカテゴリに分類して状況を把握したい場合はこのプロットを使うと効率的に可視化できます。

plt.figure(figsize=(16,16))

g = sns.factorplot(x="Generation", y="Sp. Atk", hue="Legendary", data=pkmn, kind="lv", col="Type 1", col_wrap=3 

 

タイプ毎に分けたプロット領域に、世代/伝説であるかどうかを分けてグラフを一度に描画しています。

colに"Type 1"を指定してタイプごとに分かれたプロット領域を一直線に並べ、 col_wrapを4に指定することで、4つごとに改行させています。

プロットのタイプにはpoint, bar, count, box, violin, strip, lvといった、Categorical Plotのメソッドを選択することができます。

 

lmplot

plt.figure(figsize=(16,16))

g = sns.lmplot(x="Attack", y="Sp. Atk", data=pkmn, col="Generation", col_wrap=3)

 

先程のfactorplotがCategorical plotsを一度に展開するものだったとすれば、lmplotはRegression plotsを指定した要素分類ごとに一度に描画するもの、と考えて良いと思います。

上記では世代毎のAttackとSp. Atkの回帰線付きの散布図にしました。col, row, col_wrapあたりの使い方はfactorplotと共通しています。また、回帰アルゴリズムの選択方法等はregplotと同様です。

Pairgrid & pairplot

実質的にはPairgridを継承したpairplotを使うことが多いと思われるため、一緒に記載します。 Facet Gridと同様、Pairgridで描画したsubplotにmatplotlibを使って直接様々なグラフを描画することも可能です

plt.figure(figsize=(16,16))

#d = pkmn.loc[pkmn.columns.isin(["HP", "Attack", "Sp. Atk", "Defense", "Sp. Def", "Speed"])]

d = pkmn[["HP", "Attack", "Sp. Atk", "Defense", "Sp. Def", "Speed"]]

g = sns.pairplot(data=d)

 

pairplotは与えられたデータの変数の要素の交差表を自動的に作成し、

• 同一データ同士の交差する点（対角線）についてはヒストグラム
• 異なるデータ同士が交差する点については散布図

を描画します。

上記では6種のステータスを取り出し、pairplotをしています。 異なるステータスが重なっている箇所では散布図が、同じステータス同士が重なっている箇所ではヒストグラムが描画されているのがわかると思います。

また、ヒストグラムと散布図が描画されている箇所はそれぞれkde、regressionで置き換えることも可能です。

pairplotは素性の分からない多数の種類のデータが与えられた時に、それぞれのデータ系列同士の相関性などを確認する上でとても有用になります。

In [37]:

plt.figure(figsize=(16,16))

d = pkmn[["HP", "Attack", "Sp. Atk", "Defense", "Sp. Def", "Speed"]]

g = sns.pairplot(data=d, kind="reg", diag_kind="kde")

 

 

JointGrid & jointplot

JointGridとjointplotもPairGrid&pairplotと同様、一緒に記載します。 FacetGridやPairGirdと同様、JointGridで作ったsubplotにmatplotlibでグラフを描画することも可能ですが、本稿はseabornに限定するため省略します。

plt.figure(figsize=(16,16))

g = sns.jointplot(x = pkmn["HP"], y = pkmn["Attack"]) 

jointplotは2種類の連続値を受け取り、それぞれ片方ずつのヒストグラムと、両方を組み合わせた散布図を描画します。

散布図が描かれている部分については、kindによって各種散布図(“scatter” | “reg” | “resid” | “kde” | “hex”)を パターン指定できます。

plt.figure(figsize=(16,16))

g = sns.jointplot(x = pkmn["Defense"], y = pkmn["Sp. Def"], kind="hex") .set_axis_labels("Defense", "Sp.Defense")

 

*1:19,19

seabornによる統計データ可視化（ポケモン種族値を例に）(1)

データの可視化をまとめて学んでおこうと思って書きました。

はじめに

データ分析はデータの可視化から

機械学習や統計分析をするに当たって、データの可視化は

• 対象のデータに対して洞察を深める
• 処理の結果を評価する
• 成果を分かりやすく他人に説明する

など、様々な局面で重要になります。

KaggleのKenel (分析/処理の過程をまとめたもの) をみても対象のデータに対する洞察を行う過程が全体の半分以上を占めていることが少なくありません。データを正しく可視化することは、データ分析や機械学習全般の土台にあたる作業です。

今回は、データの統計的可視化でよく使われるライブラリ "Seaborn" を用いてよく使う可視化パターンについてまとめてみます。

環境とデータ

実行環境にはKaglleのKernelを使いますが、オープンソースライブラリJupyterを使えばほぼおなじことが可能です。 また、ちょうど最近GoogleのG-Suiteで 公開されたColaboratory というツールでも同じように動くと思います。

https://colab.research.google.com/

また、データにはkaggleで公開されている

• Pokemon with Stats (https://www.kaggle.com/abcsds/pokemon)

を使います。

これはポケモンのステータスのデータセットです。今回の場合、データの洞察そのものが目的ではなく可視化方法の整理が目的なので、前処理無しで使えてできるだけ平易なデータを用いました。（あと、みんなもうアヤメの花びらの長さや幅は飽きてると思うので） 

準備

必要となるライブラリの読み込みます。

• numpy: 行列式を扱うためのライブラリ
• pandas: csv形式のような表データを扱うためのライブラリ
• matplotlib: グラフを描画する基本となるライブラリ(seabornはmatplotlibのラッパーとして動作)
• seaborn: 今回のメインとなる統計データをグラフ化するライブラリ

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

%matplotlib inline

import seaborn as sns 

データを読み込んで利用準備。

pkmn = pd.read_csv('../input/Pokemon.csv') 

データ最初の何例かを取り出して様子を眺める。

pkmn.head()

 

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False
3	3	VenusaurMega Venusaur	Grass	Poison	625	80	100	123	122	120	80	1	False
4	4	Charmander	Fire	NaN	309	39	52	43	60	50	65	1	False

 

ID、名前、タイプ1、タイプ2、ステータス合計、HP、攻撃力、防御力、特攻、特防、素早さ、初登場世代、伝説のポケモンであるか否かという構成になってることがわかります。

以下、Seabornでデータを可視化していきます。 

Seabornのメソッドやクラスの分類について

SeabornはMatplotlibのラッパーライブラリで、Matplotlibに比べて直感的にグラフを描くことができます。

SeabornのAPI reference: https://seaborn.pydata.org/api.html

上記を見ると、大まかに「〜Grid」というクラスと、「〜plot」というメソッドに分かれているのがわかると思います。 〜plotは変数やオプションを与えて簡易にグラフを描画することができます。さらにグラフを精密に作り込みたいときは〜Gridクラスを使って枠を作り、.plotメソッドでデータ描画していくという生のmatplotlibに近い使い方が出来るようになっています。

また、各メソッドは大まかな適用対象/目的ごとに大分類されているようです。 以下では、グラフ描画メソッドを大分類ごとに使っていきます。（説明の流れ上、Axis Gridは一番最後に回しています）

1. Categorical plots

対象のデータが二つの変数を持ち、片方がカテゴリ別でもう片方が連続値を持つ場合の描画に用います。(countplotを除く) 以下では、各世代(タイトルナンバリング))ごとにHPの分布を可視化していきます。 

stripplot

sns.set_style("whitegrid")

sns.set_palette("husl")

sns.set_context("notebook")

plt.figure(figsize=(15, 8))

ax = sns.stripplot(x=pkmn["Generation"], y =pkmn["HP"])

 

stripplotは素朴にstrip(細い端切れ)のように一直線上にデータをプロットします。

 

少数のサンプルに対して素朴なカテゴリごとのデータ分布を見るには良いですが、上でいう50 ~ 100の間など沢山の点が重なっている部分ではどのくらいの重なりがあるのか分かり辛いことが多いです。また、中央値等の所在も分かり辛いです。

これ単体で積極的に使うことは無いですが、他のグラフと組み合わせて使うことがあります。

第一世代と第二世代でHPが外れ値のように大きくなってるのは

pkmn[pkmn["HP"]>200]

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary
121	113	Chansey	Normal	NaN	450	250	5	5	35	105	50	1	False
261	242	Blissey	Normal	NaN	540	255	10	10	75	135	55	2	False

 

ということでChansey(和名: ラッキー) とBlissey(和名: ハピナス)のようです。実際のデータ分析でも、このようにグラフから外れ値の有無/内容を確認していく作業は重要になります。

 

swarmplot

plt.figure(figsize=(15, 8))

ax = sns.swarmplot(x=pkmn["Generation"], y =pkmn["HP"])

 

 

同じデータを可視化していきます。swarmplotはswarm(群れ)というだけあって、まるでバッファローの群れのようにパラメータの同じサンプルの分布具合が見て取れます。直感的に分布を見て取れるのが大きな利点です。

boxplot

plt.figure(figsize=(15, 8))

ax = sns.boxplot(x=pkmn["Generation"], y =pkmn["HP"])

 

boxplotはswarmplotほど直感的ではないですが、重要な統計情報がまとまっています。

中心線は平均ではなく中央値です。

それぞれのカテゴリ毎の絶対数に興味がなく、分布の偏りに対する興味が強い場合に使うと良さそうです。

violinlot

plt.figure(figsize=(15, 8))

ax = sns.violinplot(x=pkmn["Generation"], y =pkmn["HP"]) 

一見、変な形のグラフに見えますがよく見るとswarmplotの直感的な部分とboxplotの分布が定量的にが読みやすい長所を兼ね備えた優れたグラフです。名前の通りバイオリンのような形をしてます。

ただし、平滑化の過程で本来存在しない値のサンプルが存在するように見えてしまうことがあるので注意が必要です。 (例えば、[9,10,10,11,99,100,101]のような極端なデータを普通にviolinplotすると-50近辺までのサンプルが存在するかのようなグラフが描かれてしまいます)

また、Categorical plots全般ですが、hueパラメータに特定のフラグを与えることで、さらに系列を分割して比較することができます。

plt.figure(figsize=(15, 8))

ax = sns.violinplot(x=pkmn["Generation"], y =pkmn["HP"], hue=pkmn["Legendary"], split=True) 

例として、普通のポケモンのHP分布（左側）と伝説のポケモンのHP分布（右側）を比べてみました。伝説のポケモンは基本的にHPが高く設定されているようです。 

また、vionlinplotに限らずSeabornでは描くグラフは任意の他のグラフと同時に描画することができます。

plt.figure(figsize=(15, 8))

ax = sns.violinplot(x=pkmn["Generation"], y =pkmn["HP"], inner=None, color="0.95", linewidth=0.3)

ax = sns.swarmplot(x=pkmn["Generation"], y =pkmn["HP"]) 

 

swarmplotとviolinplotを組み合わせました。見やすくするためにviolinplotの色や線の太さを調整しています。 

lvplot

plt.figure(figsize=(15, 8))

ax = sns.lvplot(x=pkmn["Generation"], y =pkmn["HP"]) 

箱ひげ図と似た感じのletter value plotという方式のプロットを行います。 "letter value plot"は割りと最近になって提唱されたboxplotの改良版にあたるグラフ描画手法です。 (http://vita.had.co.nz/papers/letter-value-plot.html)

boxplotが比較的小規模なデータに対して手書きすることを前提に設計されており、大規模なデータセットに対して沢山の情報が抜け落ちてしまうという欠点を持っているのに対して、lvplotではより多くのletter value (要約値)を図に反映することができます。

実際、第3/1四分位数より上/下についても、細かに段階が付けられており大量のサンプルからなるデータの分布の特徴をboxplot以上に精密に読み取ることができます。

 

pointplot

plt.figure(figsize=(15, 8))

ax = sns.pointplot(x=pkmn["Generation"], y =pkmn["HP"]) 

pointplotは極めてシンプルな図です。 点が打たれている箇所が平均値(mean)で、線が引かれているのが95%信頼区間です。 (boxplotやlvplotは中央値(median)と第x分位数です)

95%信頼区間の95という数字や平均値の求め方については引数により制御することができます。

このグラフは情報がシンプルなので、複数の系列を比較するのに向いています。 例えば、

plt.figure(figsize=(15, 8))

ax = sns.pointplot(x=pkmn["Generation"], y =pkmn["HP"], hue=( pkmn["Type 1"].isin(["Grass"]) | pkmn["Type 2"].isin(["Grass"])), dodge=True)

 

草タイプ以外(左)と草タイプ(右)のHPの分布を比較できました。シリーズ全般を通じて、草タイプのポケモンのHPの平均は低めという傾向が読み取れます。

平均や信頼区間を簡単に比較できるので、pointplotの系列比較はわりとよく使われている気がします。 

barplot

plt.figure(figsize=(15, 8))

ax = sns.barplot(x=pkmn["Generation"], y =pkmn["HP"],  capsize=.2)

 

barplotは文字通り棒グラフです。

棒グラフの値は各データの平均値で、縦線が信頼区間なので、可視化されている情報としてはpointplotと代わりありません。ただ、見ての通り0を起点として描かれるので値全体に占める信頼区間の大きさやカテゴリ毎の平均差異が全体のうちでどのくらいなのか、という部分はpointplotより見やすいかと思います。

(capsizeを指定すると信頼区間に横棒が生えます。見やすくなるのでオススメ)

このグラフももちろんhueを指定してさらに系列分割できます。

countplot

plt.figure(figsize=(15, 8))

ax = sns.countplot(x=pkmn["Generation"])

 

 

countplotはここまでのCategorical Plotと異なり、単純に指定されたカテゴリに含まれるデータがいくつあるかをカウントします。(yを代わりに指定することもできますが、横棒グラフになるだけです。xと同時には指定できません)

上記ではGenerationを指定したので、世代毎のデータ数（つまりポケモン数）が棒グラフになっています。 このプロットは下記のようにタイプ別の数え分けに使うことが多いと思います。

plt.figure(figsize=(15, 8))

ax = sns.countplot(x=pkmn["Generation"], hue=pkmn["Type 1"], palette="Set1" )

 

"Type 1" で分類してカウントしました。色は見分けが付きやすいパレットを選択しています。 （ポケモンは属性を二つ持つので、実際には"Type 2"も勘案する必要がありますがここでは気にしない）

2. Distribution plots

カテゴリラベルではなく何らかの数量であるデータ(1変数または2変数)を可視化するために用います。 APIリファレンスと順番が異なりますが、説明のわかりやすさのためkdeplot, rugplotを先に記載し、distplotを後に記載します。 

kdeplot

plt.figure(figsize=(15, 8))

ax = sns.kdeplot(pkmn[pkmn["Legendary"]==False]["Total"])

 

変数列を1つ、または2つ受け取り、対象のデータを元にカーネル密度推定（KDE: Kernel Density Estimation）を行い、その結果をプロットします。（つまり、平たく言えば「変数の分布を確率分布に変換」します） 結果として確率密度関数が描かれることになるので、全体を積分した値は常に1となります。

ここでは伝説のポケモンを除くポケモンの、パラメータ値合計("Total")でplotしてみました。例えば、伝説でないポケモン全部から一体をランダムに選ぶと、このKDEで変換した確率密度関数で計算するとHP種族値が500ぴったりのポケモンを引く確率は約3.8%程度となります。

プロットの使い途としては、サンプルデータを確率密度関数に変換する時に分布の様子をみたり下記のようなパラメータを調整したりするために使うことが多いと思います。

KDEは以下のような式で算出される関数です。

 

ただし、n: データ数, h: バンド幅, K: カーネル関数

バンド幅hhを小さい値にするほど分布の細かい特徴が反映されやすく、逆に大きくするほど平滑になります。(標準では自動的にバンド幅を選択するアルゴリズムが選択されています)

カーネル関数Kには標準ではガウスカーネルが選択されていますが、別のカーネル関数を指定することもできます。

# バンド幅を10と指定した場合

plt.figure(figsize=(15, 8))

ax = sns.kdeplot(pkmn[pkmn["Legendary"]==False]["Total"], bw="10")

 

kdeplotでは、1変数ではなく2変数を指定することもできます。

plt.figure(figsize=(10, 10))

ax = sns.kdeplot(pkmn["Attack"], pkmn["Sp. Atk"], shade=True) 

攻撃力と特殊攻撃力を2変数としてみました。色の濃い所が確率密度の高いところです。(shadeを指定しないと等高線表示になります)

この場合、値が大きい方に行くに従ってSpかAtkのどちらかに分かれていき（相関が弱くなっていき）、全体が三角形に近い形になっている様子を見て取ることができます。

 

rugplot

plt.figure(figsize=(15, 8))

ax = sns.rugplot(pkmn[pkmn["Legendary"]==False]["Total"])

 

rugplotはカテゴリが一つしかないときのstripplotと同じようなもので、各データを単に一本一本の棒で描画していきます。

kdeの最初の例と同じく伝説以外のポケモンのステータス合計値をデータとしました。

rugplotは単体でつかうことはあまりないと思います。後述のdistplotなどと合わせて補助的にデータの分布を可視化するたに使うことが多いと思います。

distplot

plt.figure(figsize=(15, 8))

ax = sns.distplot(pkmn[pkmn["Legendary"]==False]["Total"])

distplotは指定した1変数の分布を可視化します。ここでは伝説のポケモンを除くポケモンの、パラメータ値合計("Total")でplotしてみました。

distplotはごくシンプルに指定された変数のヒストグラムを描画し、合わせてkdeやrugを一緒に描画してくれます。 kdeやrug, ヒストグラムはそれぞれオプションでon / offできます。

plt.figure(figsize=(15, 8))

ax = sns.distplot(pkmn[pkmn["Legendary"]==False]["Total"], kde=False, rug=True)

 

つづきはこちらです

mizti.hatenablog.com

chainer: トレーニングモジュールの拡張方法まとめ

chainerのチュートリアルをこなしたあと、

• mnistなどライブラリが標準で用意してる以外の独自データセットをどうやって作ったら良いんだろう？
• 複数のモデルが絡むネットワークを同時並行に訓練/評価するにはどうすれば？

といった点で困ることが多くありました。

結果的にはChainerのトレーニング関係のコンポーネントを拡張/自作するのが良さそうなのですが、 それぞれにちょっとずつポイントが有ります。ここでは、トレーニング関連のオブジェクトを概観しながら 今までに書いてきたエントリをまとめます。（今後も増えるかも..）

chainerのトレーニング関連コンポーネント概観

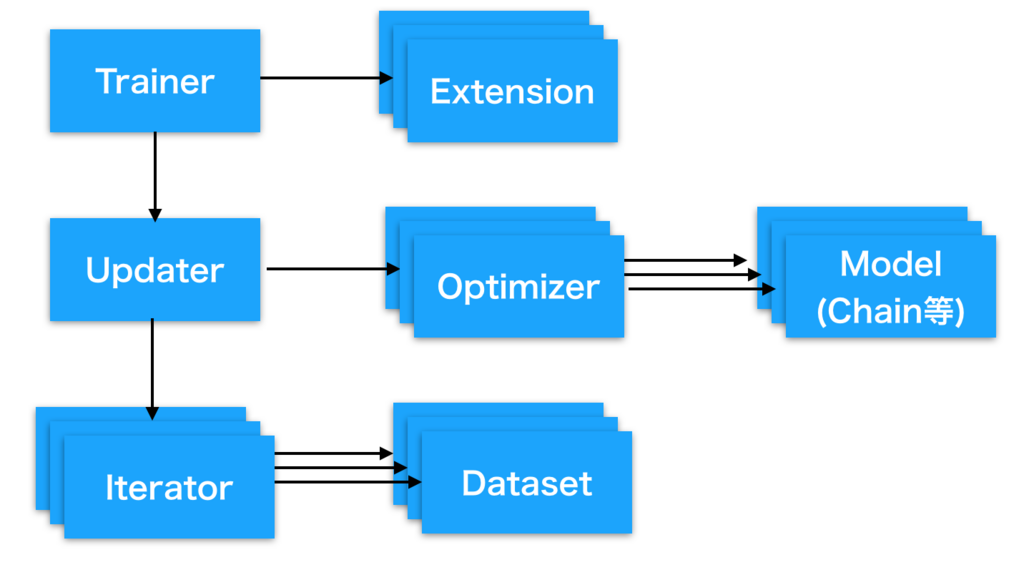
Trainer:

登録されたUpdaterを使って指定したepoch数やイテレーション数分だけ訓練を実行します。

Extensions:

Trainerが実行される過程で付属的に実行される処理を規定します。

mizti.hatenablog.com

モデルの評価を行うEvaluatorもExtensionの一種として定義されます。

mizti.hatenablog.com

Updater:

Datasetを含むIterator、訓練対象のモデルオブジェクトと勾配更新方法を規定するOptimizerを受け取って、 具体的にどのようにモデル群を更新していくかを規定します。

mizti.hatenablog.com

Optimizer:

SGD, Adamなど勾配計算後のパラメータ更新方法を規定します。

Model (Link / Chain)

ニューラルネットワーク(NN)の本体です。基本的にはLinkやFunctionを積み重ねてChainでラッピングしNNを構成していきます。 （Chain自体もLinkを継承して作られたLinkオブジェクトの一種なため、ChainとChainを繋いだりChainとLinkを繋いだりもできます）

Datasetと合わせてLinkやChainで作られるChainerのNNの概要を図にまとめてみました。

Iterator:

下記のデータセットを受け取り、ミニバッチサイズや取り出し順のポリシーを設定します。

Dataset:

画像などのデータとラベルの対を多数保持します。下記のエントリーでまとめたように、 Datasetクラスを継承することで極めて簡単かつ柔軟に定義できます

mizti.hatenablog.com

chainer: Evaluatorを自作してトレーニング中のモデルの評価を柔軟に行う

Evaluatorとは

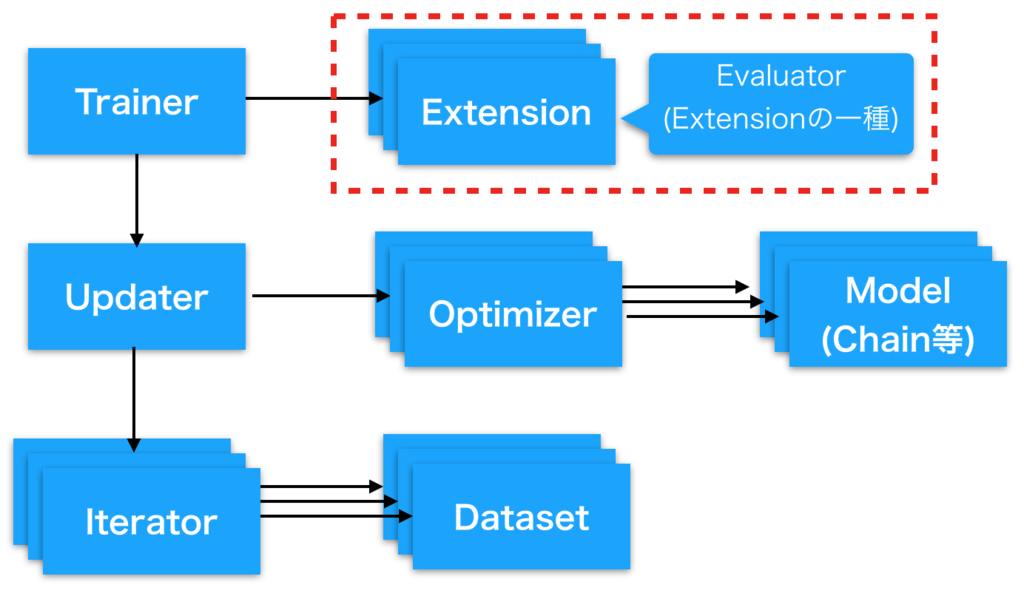
DNNの訓練を行う中でモデルの訓練が意図通り進んでいるかを評価したくなることが多いと思います。

Chainerでは定義したモデルの訓練を行う際にそのモデルの評価を行うための仕組みとしてEvaluatorという 仕組みを持っています。

このEvaluatorは 以前解説したExtensionの一種として作られています。

本質的にはExtensionを自分で自作すればモデルの評価ももちろん可能なのですが、 Evaluatorを継承してカスタマイズすることでaccuracyやlossの計上、イテレータの状態管理などをスマートに行うことができます。

chainer 標準のEvaluator

まず、継承元になるEvaluatorの作りを確認してみましょう。 Evaluatorについては、chainer標準のextensions.Evaluatorがかなり汎用的に作られており、自作せずに済むのならそれに越したことはないので。

Trainer extensions — Chainer 2.0.0 documentation

Evaluatorは、まず下記のようなオブジェクトを受け取ります。

• iterator: 評価用のデータセット、ミニバッチサイズ等が設定されたイテレータオブジェクト
• target: 評価対象となるモデル、もしくはモデルの列挙されたdict。
• converter: イテレータから取り出した(データ, ラベル)のタプルを訓練用のミニバッチに変換する関数
• device: 評価計算を行うために利用するGPU番号
• eval_hook: 評価前に実行される関数(なくてもok)
• eval_func: 評価を行うために呼び出される関数 (指定されない場合、targetに渡したモデルのcallが代わりに利用される)

chainer.training.extensions.evaluator — Chainer 2.0.0 documentation

で、それぞれ主要なメソッドの動作をざっくり確認すると

• __init__ :
  • 渡された引数をインスタンス変数として格納する。
  • 特に、targetにモデルのdictではなく単一のLinkが渡された場合、そのlinkを"main"という名前で辞書登録しなおす
• __call__:
  • Reporter objectを作成して、targetとして渡された各リンクのを監視対象に指定する。
  • evaluateメソッドを呼び出し、その結果をreporterを使ってreportする。 (__call__の戻り値は参照されておらず、reporter_module.reportに渡したdictが印字対象な点に注意)
• evaluate:
  • 渡されたiterator("main")からbatchを取り出す
  • 渡されたモデル("main")、もしくはeval_funcにbatchから取り出したデータ/ラベルを入力する(ここでobserverにaccuracy/lossが記録される)
  • observerに書かれたaccuracy/lossをsummaryに蓄積。
    • summaryはDictSummaryのインスタンス。DictSummaryはキー毎に投入された値の回数や平均値、二乗和を蓄積でき、平均や分散などの統計値を取り出せます
  • 最後にsummaryに蓄積された値を平均して呼び出し元(__call__)に返却

ということをしています。

つまり、標準のEvaluatorではこういうことが可能です。

• 単一のモデルと単一イテレータの評価。
• モデルのcallを評価対象にしても良いし、eval_funcで関数を渡して評価に使っても良い

標準のEvaluatorは複数のモデルをtargetに辞書として受け取ることはできますが、 evaluateメソッドが'main'のみを用いて評価するようになっているため、複数のモデルを評価に用いることはできません。

Evaluatorを自作する

逆に標準のEvaluatorではできないこと、例えば

• 複数のモデルやイテレータを使った評価(たとえばGANのGeneratorとDiscriminatorなど)
• accuracyやloss以外の指標値の出力(一応、eval_funcを使えば可能ですが)

などがしたい場合にはEvaluatorを自作すると良いかと思います。 Updaterの自作をした場合には対応するEvaluatorを作りたいことが多いかと思います。

拡張例

様々な拡張方法があると思いますので、やりたいことベースでchainer標準のEvaluatorを継承して独自のEvaluatorを定義する幾つか例を挙げていきます。

①とにかく指定した値をログやレポートに表示させたい

印字させたい項目を項目名をkey、スカラー値をvalueに持つ辞書をreporter_module.reportに渡せば、 とりあえず指定した値をログやレポートに表示させられます。

from chainer import reporter as reporter_module
from chainer.training import extensions

class MyEvaluator(extensions.Evaluator):
    def __call__(self, trainer=None):
        result = {"hoge": 4, "piyo": 88}
        reporter_module.report(result)
        return None

出力:

    {
        (略)
        "hoge": 4.0,
        "piyo": 88.0
    }

chainerのReportで受け取る辞書(dict)の各値はスカラー値であることが必須です（文字列やリストは渡せません）。

②複数のモデルを用いて評価を行う

影響しあう複数のモデルを並列に訓練しているなどで評価を行いたい場合、 evaluateでtargetに指定するモデルをself._targetsから取り出す際に指定するorループで順に呼び出すなどすると良いと思います。

呼び出し元:

trainer.extend(MyEvaluator(test_iter, {"model1": model, "model2":model2}, device=args.gpu))

Evaluator側:

class MyEvaluator(extensions.Evaluator):
    default_name="myval"
    def evaluate(self):
        #target = self._targets['main']

        summary = reporter_module.DictSummary()
        for name, target in six.iteritems(self._targets):
            iterator = self._iterators['main']
            #target = self._targets['main']
            eval_func = self.eval_func or target

            if self.eval_hook:
                self.eval_hook(self)

            if hasattr(iterator, 'reset'):
                iterator.reset()
                it = iterator
            else:
                it = copy.copy(iterator)

            #summary = reporter_module.DictSummary()
            for batch in it:
                observation = {}
                with reporter_module.report_scope(observation):
                    in_arrays = self.converter(batch, self.device)
                    with function.no_backprop_mode():
                        if isinstance(in_arrays, tuple):
                            eval_func(*in_arrays)
                        elif isinstance(in_arrays, dict):
                            eval_func(**in_arrays)
                        else:
                            eval_func(in_arrays)

                summary.add(observation)
        return summary.compute_mean()

色々書いてあるように見えますが、元のevaluate()からの変更点は

1. クラス変数default_nameを指定している(下記のログ出力のようにReporterがログ項目の接頭辞にしてくれます)
2. target = self.targets['main']ではなくself.targetsからループで取り出すようにしている
3. summaryの宣言をそのループの外側に書いた

だけです。

self._targetにはEvaluator定義時に指定したモデルが入っているのですが、

• 単一のモデル渡す（そのモデルが"main"という名前で__init__内で辞書登録される）
• モデルを辞書で渡す

のどちらでも良いようになっています。

このようにすることで

    {
         (略)
        "myval/model1/loss": 0.07286249771073926,
        "myval/model1/accuracy": 0.9748000055551529,
        "myval/model2/accuracy": 0.0888000001013279,
        "myval/model2/loss": 2.3258586740493774
    }

のように各モデルに対する評価を出力できます。

③モデルの評価中に独自指標値を出力

Inceptionのように一つのモデルから複数の出力がある場合など、accuracyとloss以外の指標を計測してログに出力したいことも多いと思います。そのような場合には

    def evaluate(self):
        iterator = self._iterators['main']
        target = self._targets['main']
        eval_func = self.eval_func or target

        if self.eval_hook:
            self.eval_hook(self)

        if hasattr(iterator, 'reset'):
            iterator.reset()
            it = iterator
        else:
            it = copy.copy(iterator)

        summary = reporter_module.DictSummary()

        for batch in it:
            observation = {}
            with reporter_module.report_scope(observation):
                in_arrays = self.converter(batch, self.device)
                with function.no_backprop_mode():
                    if isinstance(in_arrays, tuple):
                        eval_func(*in_arrays)
                    elif isinstance(in_arrays, dict):
                        eval_func(**in_arrays)
                    else:
                        eval_func(in_arrays)

            summary.add({MyEvaluator.default_name + '/currenttime': int(time.time())})
            print(observation)
            summary.add(observation)

        return summary.compute_mean()

• summary.add({MyEvaluator.default_name + '/currenttime': int(time.time())})を足しています

これはreporter_module.report_scope(observation)のスコープ内でchainer.reporter.report(dict)が呼び出されると、 observationにdictが追加されるという仕組みを用いています

例ではUnixtimeをログに出していますが、モデルや出力に関する適切な数値を渡すことで 評価中のモデルについて都合の良い指標を出力できます。

（私の場合だと例えば、文字列を認識するモデルに対して正解文字列までの編集距離を出力するのに使っていました)

④GANのUpdater / Evaluator

下記の記事がGAN用のUpdater / Evaluatorの対の実装例になっているので、GANを実装したい方は参考に できると思います。

qiita.com

---

chainerで少し複雑なモデルを初めて扱うことになると評価をどうしようか迷うと思いますが(実際迷いました)、このようにEvaluatorを拡張することで柔軟に対処できるようになるかと思います。

chainer: Extensionを自作してディープラーニングの訓練に独自処理を挟み込む

なぜExtensionを自作するのか

Chainerのモデルのトレーニング中に、

• たまにモデルの出力をダンプさせたい（特に生成系で必要になる）
• 1エポック毎に学習率を手動で変更したい

など、独自の処理を定期的に挟みたくなることがあるかと思います。 このような願いを叶えるのがchainerのextensionという仕組みです。 extensionはtrainerに仕掛けておくことで指定した間隔ごとに独自に定義した処理を実行してくれます。

extensionはtrainerにひも付き、一つのtrainerにいくつでもextensionを設定することができます。

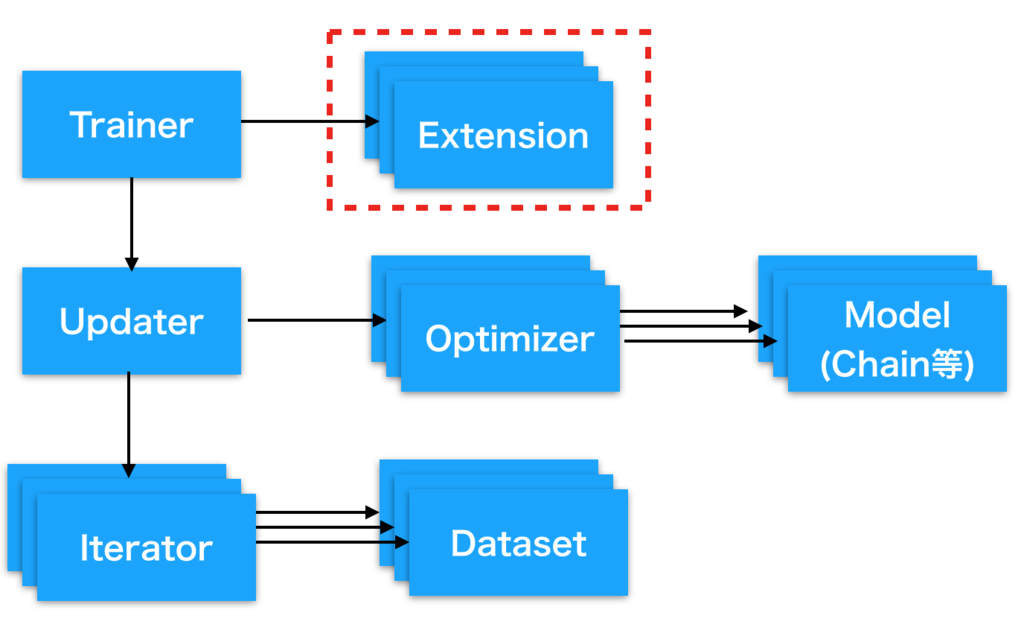
Extensionの自作方法

モデルを定期的に評価するEvaluatorもこのextensionを使って実装されています。 モデルの評価用途にはこのEvaluatorを拡張したほうが早いでしょう。 ここでは評価以外のより一般的にextensionを自作する方法にフォーカスします

例えば、公式ではこのようなExtensionが用意されています。よく使うのはこのあたりでしょうか。

Extension名	概要
extensions.Evaluator	モデルの損失や正解率を評価する
extensions.snapshot	モデルの重みをファイルに保存する
extensions.LogReport	Evaluator等で測定した各種の評価値をログに出力する
extensions.PrintReport	指定した評価値を標準出力やファイルに出力する

これらの公式Extensionはチュートリアル等でも言及されていますが、 extensionは簡単に自作することも可能です。

簡単なextensionの例として、「"hoge"とpirntするだけ」のextensionを作ってみましょう。

main.py
   |
   + lib -- print_hoge.py

このようなディレクトリ構成で、 定義側(print_hoge.py):

print_hoge.py
def print_hoge():
    @training.make_extension(trigger=(1, 'epoch'))
    def _print_hoge(trainer):
        print("hoge")
    return _print_hoge

呼び出し側 (main.py):

from lib.print_hoge import *
(略)
trainer = training.Trainer(updater, (30, 'epoch'), out=args.output)
trainer.extend(print_hoge())

たったこれだけの記述で、1epochに一回、hogeと標準出力に出力されるようになります。

Extensionのカスタマイズ

動作する間隔を変えたければ

 - trigger=(1, 'iteration'): 1イテレーションに1回
 - trigger=(3, 'epoch'): 3エポックに一回

などtriggerを変更すればokです。 また、extensionの中でモデルを参照したければtrainer.update.modelとういうように、 trainerに登録されたupdater経由でアクセス可能です。

下記のように実行時に引数を与えることも可能です。

print_hoge.py
def print_hoge(message):
    @training.make_extension(trigger=(1, 'epoch'))
    def _print_hoge(trainer):
        print(message)
    return _print_hoge
呼び出し側 (main.py)
from lib.print_hoge import *
(略)
trainer = training.Trainer(updater, (30, 'epoch'), out=args.output)
trainer.extend(print_hoge("fuga"))

後はextension名と中身の処理を好きなように書き換えればokです。

---

以下はもう少し詳しく知りたい方向け

書き方のポイントは、関数print_hoge()が関数「_print_hoge」自体を返り値に返却していることです。 実際、「関数を返却する関数」を定義しなくても

print_hoge.py
@training.make_extension(trigger=(1, 'epoch'))
def print_hoge(trainer):
    print("hoge")

と定義して、呼び出し側(main.py)で

from lib.print_hoge import *
(略)
trainer = training.Trainer(updater, (30, 'epoch'), out=args.output)
trainer.extend(print_hoge)

とtrainer.extendに関数を直接渡せば最初の例と同じように動作します。 （trainer.extend(print_hoge())ではなくtrainer.extend(print_hoge)となっていることに注意してください)

上記のようにも書けるのですが、chainerの公式コードでは一度「関数を返す関数（ないしクラス）」を使う実装がなされています。 これは外側の関数(print_hoge)を関数と内側の関数(_print_hoge)の間で変数を定義することで_print_hogeで参照する変数のクロージャを作ることができ、色々便利だからかと思います。

また、

@training.make_extension(trigger=(1, 'epoch'))
def print_hoge(trainer):
    print("hoge")
@training.make_extension(trigger=(1, 'epoch'))

という処理も一見何か難しいことをしているように見えますが、 make_extension関数内で行われていることは下記とほぼ同義です。

def sample_recog(trainer):
    print("hoge")

sample_recog.trigger=(1, 'iteration')

つまり、極端な話

def sample_recog():
    def _sample_recog(trainer):
        print("hoge")
    _sample_recog.trigger=(1, 'iteration')
    return _sample_recog

このように定義してもmake_extensionを使ったときと同じように動きます。